Discrete Curvature and Machine Learning on Graphs
Complex Networks are popular means for studying a wide variety of systems across the social and natural sciences. In a series of articles, we developed geometric tools to describe the structure and evolution of such networks. The core component of our theory, a discrete Ricci curvature, gives rise to two geometric flows that allow for an edge-based network analysis. Thus we extend the commonly used node-based approach to include edge-based information such as edge weights and directionality for a more comprehensive and computationally efficient characterization of networks.
The analysis of a wide range of complex networks suggests connections between curvature and higher order network structure. As a proxy for local assortativity, curvature identifies long-range connections that act as bridges between major network components. By identifying higher order structural features we characterize and classify the network’s geometry.
Selected Works
- Y. Tian, Z. Lubberts, M. Weber (2023): Curvature-based Clustering on Graphs. Under Review
- N. García Trillos, M. Weber (2023): Continuum Limits of Ollivier's Ricci Curvature on data clouds: pointwise consistency and global lower bounds. Under Review.
- L. Fesser, S. Serrano de Haro Iváñez, K. Devriendt, M. Weber, R. Lambiotte (2023): Augmentations of Forman's Ricci Curvature and their Applications in Community Detection. Under Review.
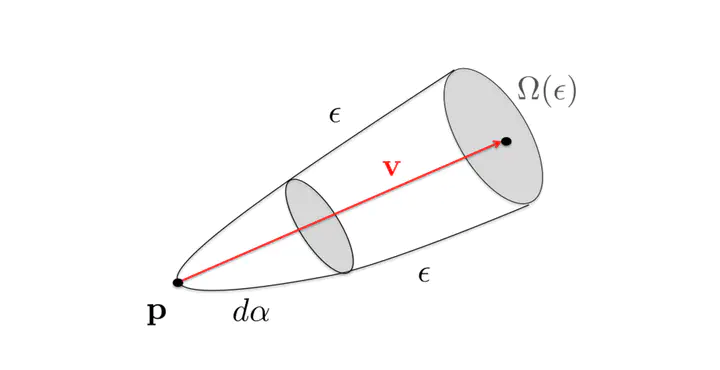
- M. Weber (2020): Neighborhood Growth Determines Geometric Priors for Relational Representation Learning. AISTATS
- E. Saucan∗, M. Weber∗ (2019): Forman’s Ricci curvature – From networks to hypernetworks. 7th Conference on Complex Networks and Their Applications. (*: co-first authors)
- M. Weber, E. Saucan and J. Jost (2017): Coarse Geometry of Evolving Networks. Journal of Complex Networks, vol. 6(5), pp. 706-732.
- M. Weber, E. Saucan and J. Jost (2017): Characterizing Complex Networks with Forman-Ricci Curvature and Associated Geometric Flows. Journal of Complex Networks, vol. 5 (4), 527-550.
- M. Weber, J. Jost and E. Saucan (2016): Forman-Ricci flow for change detection in large dynamic data sets. Axioms, vol. 5 (4).